| E0407 |
Le noeud papillon.
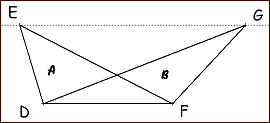 Observons les triangles EDF et GDF : ils ont la même base et la même hauteur. En conséquence ils ont la même aire. Or ces deux triangles ont une partie commune. Une fois cette aire commune retirée, nous obtenons les aires A et B. On peut donc conclure que A = B.
|
| E0408 |
1, 2, 3,… ou bien cinq, deux, dix…
C’est 20.
Ecrivons en lettres les nombres de 1 jusqu’à 20 :
Cinq, deux, dix, dix-huit, dix-neuf, dix-sept, douze, huit, neuf, onze, quatorze, quatre, quinze, seize, sept, six, treize, trois, un, vingt.
Le nombre 20, écrit vingt, apparaît bien en 20ème position mais 1 apparaît en 19ème position ! 2 en 2ème position,…
Ecrivons en lettres les nombres de 1 jusqu’à 10.
Cinq, deux, dix, huit, neuf, quatre, sept, six, trois, un.
1 apparaît maintenant en 10ème position !!!
Et en écrivant en lettres les chiffres de 1 jusqu’à 35, alors 1 vient en 25ème position.
C’est si simple d’écrire les nombres consécutifs en chiffres, mais en lettres, non ! et repérer leurs rangs demande aussi un autre travail ! |
E0409
|
Proverbe dissimulé.
Ce proverbe célèbre est évidemment « Tout ce qui brille n’est pas or ».
Le quatrième mot de ce proverbe est donc : BRILLE .
|
| E0410 |
Bonus spécial 2005.
Le savant dont on vous demandait le nom est Einstein
(Nous recommandons à votre professeur la lecture d’un ouvrage récent publié en 2004 chez l’éditeur Ellipses. Jean Hladik : Comment le jeune et ambitieux EINSTEIN s’est approprié la Relativité restreinte de POINCARE).
Nous vous avons aussi fourni la célèbre égalité E = m c2 en vous demandant de réfléchir à ce qu’elle signifiait.
Cette simple formule peut se lire : L'énergie (E), EST de la matière (« m » signifie masse) ou bien : la matière EST de l'énergie.
Elle permet de calculer ce changement de l'état matière en l'état énergie (la « transformation » ) d'une certaine quantité de matière donnée par sa masse en énergie (par exemple celle d'une quantité d'uranium dans un réacteur nucléaire).
Calculons cette énergie en un temps donné et nous pourrons alors parler de « puissance ». Les unités sont exprimées ici dans le Système International d'unités (SI) , c'est à dire le temps exprimé en secondes, la puissance ( de l'énergie produite en un certain temps ) en watts, la masse (m) en kilogrammes, et c représente une constante (la célérité ou vitesse de la lumière) qui est 300 000 000 m/s) ; la constante c2 dans le SI, c'est donc un 9 suivi de 16 zéros !!
La transformation en énergie d'un kilogramme de matière, en un temps d'une seconde, fournit (dans le cas d'une centrale nucléaire par exemple) une énergie de 90 000 000 de Gw (le gigawatt vaut le milliard de watts).
Recherchez maintenant les puissances fournies par nos centrales thermiques ou celles consommées par divers moteurs, foyers domestiques, . L'énergie du soleil a sa source dans de telles transformations.
|
| PC0407 |
Le pavé dans la mare.
Il peut construire 10 pavés différents : les différents volumes en sont : 1×1×60 ; 1×2×30 ; 1×3×20 ; 1×4×15 ; 1×5×12 ; 1×6×10 ; 2×2×15 ; 2×3×10 ; 2×5×6 ; 3×4×5.
La plus petite surface possible s’obtient avec le pavé le plus « compact » :
S = 2 × ( 3×4 + 3×5 + 4×5 ) = 2 × (12 + 15 + 20 ) = 2 × 47 = 94.
La plus grande surface possible s’obtient avec le pavé le plus «allongé» :
S = 2 × ( 1×1 + 1×60 + 1×60 ) = 2 × ( 1 + 60 + 60 ) = 2 × 121 = 242.
|
| PC0408 |
La bande.
Le « 1 » est déjà fort heureusement placé. Il suffit alors de quelques essais pour obtenir :
23 + 45 + 1 + 9 = 78.
Sur le morceau restant, le nombre écrit est le « 6 ».
|
| PC0409 |
Une simple multiplication...
A = 1, M = 2, H = 8, T = 7
Tout d’abord, une première remarque : il n’y a pas de retenue pour M × 4 puisqu’on obtient H.
M est donc égal à 1 ou à 2.
Or, deuxième remarque, H × 4 est un nombre qui se termine par M. Aucun résultat dans la table de multiplication par 4 ne se termine par 1 et donc M = 2 . En conséquence H = 8 ( il faut éliminer la valeur 9 pour H car 9 × 4 = 36 qui ne se termine pas par 2 ).
A ne peut être égal qu’à 1 puisque A × 4 se termine par le chiffre T et qu’il n’y a pas de retenue pour la multiplication suivante.
T × 4 se termine donc par 1 mais il y avait 3 en retenue ; la seule réponse posssible est donc T = 7 puisque 7 × 4 = 28 et 28 + 3 = 31.
Nous avons enfin : A × 4 qui donne 7. C’est bien cela puisque 1 × 4 = 4 et 4 + 3 = 7.
Math s’écrit donc en chiffre : 2178 ( et Math × 4 = 2178 × 4 = 8712 ).
|
| GC0409 |
Décimale cachée.
1/81 = 0,012 345 679 012 345 679 012 345 679 012 345 679 012 345 679 012 3 ...
On remarque une période de 9 chiffres : 012345679
Or 818 181 / 9 = 90 909, cette division tombe juste et donc il y aura 90 909 segments de 9 chiffres pour obtenir la 818 181 ème décimale de 1/81 .
Cette décimale est donc un 9.
|
| GC0410 |
Un simple calcul.
A x B = 1 .
|
| GC0411 |
De 2 en 2.
Aucune difficulté pour résoudre ce petit texte ; il suffit d’écrire les nombres barrés au premier tour :
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51
53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99
Puis de faire un second tour en barrant les nombres comme précédemment :
2 6 10 14 18 22 26 30 34 38 42 46 50 54 58 62 66 70 74 78 82 86 90 94 98
Un 3ème tour et je barre :
4 12 20 28 36 44 52 60 68 76 84 92 100
Au tour suivant, je barre :
16 32 48 64 80 96
puis je barre :
24 56 88
enfin, le 40 et le 8.
Il me reste 72 qui est la réponse.
 Nous vous avons proposé un cadran de 1 à 100. Savez-vous que pendant la Révolution française, le jour n’était plus divisé en 24 parties, chacune en 60,… mais au contraire divisé par 10 et 100,… Nous pourrions appeler ces unités le décijour et le centijour. Voulez-vous que l’on parle de cela ? Demandez-le nous !
Et si ce petit texte vous a semblé intéressant, alors proposez-le à un ami avec un autre cadran numéroté de 1 à 1000 par exemple. Bon courage ! |
