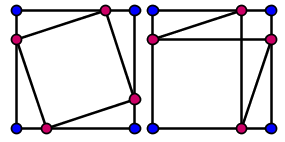
Le pont aux ânes est le nom que l’on donnait jadis, en France, au célèbre théorème de Pythagore, et, celui qui ne pouvait passer ce théorème n’était donc qu’un âne qui n’aurait pas su traverser un pont. Voici dans sa simplicité qui fait son élégance ce théorème : Dans un triangle rectangle, l’aire du carré construit sur l’hypoténuse égale la somme des aires des carrés construits sur les côtés de l’angle droit. Voici une démonstration, muette, la plus simple :

Nous vous parlerons dans un autre article (T 99) de Pythagore, vous proposerons d’autres démonstrations (dans son livre justement célèbre, «  The Pythagoren proposition », Elisha S. Loomis vous en propose pas moins de 367. Comme vous voyez, nous aurons le choix), vous parlerons aussi de triplets pythagoriciens, et  nous répondrons aussi aux petits problèmes de ce jour.

Problème 1 Découper cette croix en deux coups de ciseaux pour obtenir un carré

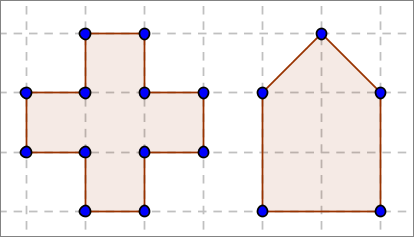Problème 2 Découper cette maison en deux coups de ciseaux pour obtenir un carré

Problème 4
Le puzzle de Pythagore ; il vous est présenté dans le fichier pdf suivant (nécessite Acrobat Reader, disponible gratuitement sur le site d'Adobe)