Ce n’est pas dans sa somptueuse cabine à ciel ouvert de Diogène que notre capitaine a fait tous ses calculs. Non, c’est bien de son bureau, sur Terre ; et bien entendu, il a utilisé la magnifique « calculatrice de Romain », ce merveilleux outil qu’il a découvert sur le site de l’ADCS et qu’il a, comme vous et moi, téléchargé.

Et puis, studieusement il a réétudié comme un bon lycéen, sa géographie en téléchargeant le document « Représenter la Terre » (fichier pdf) qui est un magnifique « travail dirigé » écrit pour des élèves de seconde , mais consultable dès que l’on sait ce qu’est un sinus et un cosinus ; et vous retrouverez sur celui-ci notre cher capitaine Haddock !

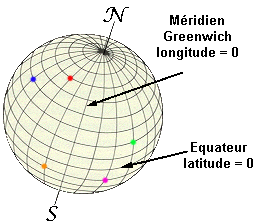Vous savez ce que sont longitude et latitude ; ces données permettent de situer exactement tout point de notre Terre et Serge grâce au GPS (voir texte T 81) connaît à tout instant sa position en mer. (Ce système américain de télédétection sera(it) bientôt remplacé par un système européen : GALILEO). Mais cette exceptionnelle possibilité technique est tout à fait récente. Et la conquête d’un moyen de repérage , fiable et en mer , vaudra en 1714 la création d’un prix (le Longitude Act) de 20 000 livres pour celui qui pourrait déterminer la longitude d’un lieu à un demi degré près (cette somme est énorme et Simaan (voir bibliographie) précise que le salaire annuel de Bradley, astronome royal était de 100 livres). Il fallut à Harrison le labeur de toute une vie (il gagne cette prime en 1759) pour atteindre cet exploit (voir l’excellent livre de Dava Sobel cité dans notre bibliographie).

Hergé construit l’ histoire de Rackham Le Rouge (voir texte T 82) à partir d’un fait authentique. Jusque 1884 (Conférence internationale de Washington), les cartes utilisées par les Anglais avaient pour méridien origine le méridien de Greenwich (banlieue londonienne) et les Français utilisaient le méridien de Paris, mais d’autres le furent aussi tel celui de l’île de Fer. La croissance des échanges commerciaux mondiaux imposait une législation commune. Et c’est par 22 voix pour le choix de Greenwich, (dont l’Angleterre), 2 abstentions (La France et le Brésil) 1 désapprobation ( St Domingue) que Greenwich fut choisi pendant cette conférence comme méridien 0 ; notons cependant qu’à l’unanimité (sauf la France qui s’abstint) fut décidé de compter les longitudes vers l’Est et vers l’Ouest, et que le principe des fuseaux horaires fut adopté ; l’emploi exclusif du système métrique, création bien française, y sera fortement encouragé.

Et j’espère que l’île de Rackham vous rappellera « L’île mystérieuse »   de Jules Verne, célèbre roman où l’écrivain picard vous conte comment Cyrus Smith et sa petite poignée d’amis opérèrent pour déterminer simplement les coordonnées de cette île qui sera leur univers pour de bien longues journées.

Et quelques calculs maintenant.. Nous nous contenterons ici de donner des « formules » de calcul. Nos jeunes lecteurs à qui ce texte est destiné pourront toujours solliciter leur professeur de mathématiques (ces gens-là sont très sympathiques) pour comprendre comment elles ont été établies.

Nous noterons L et l les longitudes d’un point. Assez curieusement et malgré les recommandations de la conférence de Washington, vous verrez (par exemple sur internet) que les longitudes sont parfois comptées depuis Greenwich certes, mais de 0 à 360° vers l’Est ! (la longitude de Pointe à Pitre, 61°W 31 devient alors 298°29).

Longitude et latitude sont comptées en degrés, minutes et secondes, mais vous pouvez aisément les transformer en degrés décimaux.. Les calculs font intervenir des angles que vous mesurez soit en degrés , soit en radians et vous savez que 

180 ° = 2 π rad, soit 1° = 2 π / 180 rad ou 1 rad = 180 /2 π degrés

(remarquez que la calculatrice de Romain effectue les calculs en degrés ou en radians)

Nous connaissons bien la première définition (1791) du mètre ( il est égal à la dix-millionième partie du quart du méridien terrestre), ce qui signifie que le méridien vaut 40 000 km.

(remarquons bien que « méridien » désigne ici un cercle de la surface terrestre passant par les pôles, alors que, en cartographie ou en navigation, le méridien désigne le demi-cercle.. Mais le contexte fera toujours qu’il n’y aura pas d’ambiguïté de compréhension. Quant à cette longueur qui nous donne le mètre, elle reste théorique , et pour les géographes (voir l’IGN, Institut Géographique National), la valeur actuelle du méridien est de 40 007,864 km et celle de l’Equateur de 40 007,017 km. Oui, la Terre est ronde !

Ne confondons pas non plus le mille et le mile de nos amis de langue anglaise ;

La verticale d’un lieu P (direction du fil à plomb), c’est la direction du centre de la Terre. Ainsi deux verticales, même de deux lieux bien peu distants ne sont pas parallèles puisqu’elles se coupent au centre de la Terre (figure 1). Puisque le méridien mesure 40 000 km, les verticales d’un pôle et d’un point de l’équateur, font un angle de 90° et l’arc de méridien entre ces points est de 10 000 km. ; nouvelle division par 60. A un angle des verticales de 1° correspond un arc terrestre de 111,111 km. Et si vous divisez maintenant ces nombres par 60, vous trouverez donc que la distance de deux lieux dont les verticales font un angle de 1 minute est de 1 852m. C’est cela le mille marin ! .

Et voici une autre unité, de vitesse cette fois : le nœud ; c’est la vitesse d’un mobile qui parcourt un mille par heure (l’expression « filer » 5 ou 10 nœuds provient d’un ancien instrument de mesure des distances parcourues en mer. Un« loch », corde à nœuds régulièrement espacés  d'1/120 ème de minute, soit 15 m,  filait dans l’eau et c’est le nombre des nœuds mouillés dans un intervalle de temps bien défini qui permettait de calculer la vitesse du bateau. Avez-vous remarqué sur le site de Serge que sa vitesse journalière est donnée en nœuds)

Le mile ( enviton1609 m) est une unité qu’utilisent les Anglo-saxons et qui provient vraisemblablement d’anciennes unités romaines. Voyez donc les compteurs des voitures made in USA ou made in England !

Calculons la distance de deux points du globe.

Examinons d’abord quelques cas particuliers simples :

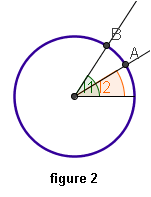- Ces deux points sont sur un même méridien (figure 2)

Appelons l1 et l2 leurs latitudes ; notons α (en radians) la différence l1 – l2

La longueur de l’arc AB est R α (R désigne le rayon de la Terre)

Un exemple :

Amiens et Paris sont sur le même méridien. La capitale de la France a pour latitude 48°,87N (= 0,853 rad ) et celle de la Picardie 49°,89 N(=0,870 rad). α = 0,017 rad; le rayon R de la terre est 40 000 km / (2π) et l’arc Amiens-Paris mesure donc 108,225 km

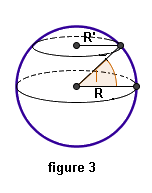
- Ces deux points sont sur un même parallèle. (figure 3)

Il nous faut d’abord connaître le rayon de ce parallèle. Appelons l la latitude d’un de ses points.. Le rayon du parallèle est alors R’ = R cos l

VILLE Latitude Latitude  degrés centésim. Latitude radians Rayon du parallèle Longueur R' du parallèle Pôle Nord 90N 90° π/2 0 km 0 km Paris 48N52' 48°,87 0,853 4 187 km 26 309 km Santa Cruz 28N27' 28°,45 0,497 5 596 km 35 161 km Pointe à P. 16N14' 16°,23 0,283 6 113 km 38 409 km Point équateur 0N 0° 0 6 366 km 40 000 km

Et si nous prenons maintenant deux points d’un même parallèle de rayon R’, points de longitude L1 et L2, nous obtenons comme précédemment la longueur de l’arc CD qui vaut R’.(L1-L2) (L1 et L2 en radians).

Exemples : 

Pour le parallèle de Paris, 2 points de longitude L1 = 40W (0,698 radian) et L2 = 30W(0,524 radians) sont à la distance d = 4 187.(0,698-0,524) km =728,54 km.

Si on était sur le parallèle de Santa Cruz, la distance serait de 973,70 km. Et sur le parallèle de Pointe à Pitre, elle serait de 1 063,66 km. Bien entendu, pour la pôle, la distance serait nulle et pour 2 points de l’équateur, d = 1 111,111 km.

- Beaucoup plus délicat maintenant.

Nos points M1 M2 de coordonnées (L1, l1) et (L2, l2) ne sont pas situés sur le même méridien, ni sur la même parallèle.

Vous pourrez vérifier que la distance (selon l'orthodromie) est alors donnée par la formule :

d = R Arcos (cos l1cos l2 cos (L1- L2) + sin l1 sin l2)

Nous pouvons alors calculer la distance entre Pointe à Pitre (L1=61°,32, l1=16°,23) et Santa Cruz (L2=16°,15, l2=28°,45). On obtient d = 4 806 km. (il s’agit donc de la distance la plus courte qu’aurait pu parcourir Serge)

Avant que de nous quitter, 2 petits problèmes : avez-vous déjà entendu dans les rumeurs océanes, l’harangue matinale très cornnélienne de Serge qu’il destine, face à l’astre du jour, à la faune qui l’environne : « A dix milles d’ici, je te le fais savoir ! « ? Oui, je suppose ! Et bien voici donc Serge, debout sur le plancher de Diogène, ses yeux étant à 1,70m du plancher (donc de l’océan). Quelle est la distance du point, à l’horizon, que peut percevoir Serge s’il est debout dans sa barque ?

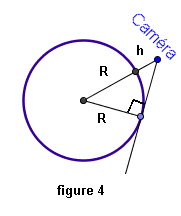Et maintenant Serge gonfle un petit ballonnet qui emporte une caméra. L’appareil est à 100 m au-dessus du niveau de l’océan. Quelle est maintenant la distance du point le plus éloigné que la caméra embarquée peut filmer ? ( figure 4) Et quelle surface d’eau peut-il filmer ?

A bientôt

bibliographie
ADAPT Editions Arkaan Simaan et Joëlle Fontaine l’image du MONDE des Babyloniens à Newton.

Voir aussi celle du texte T85

Retrouvez Serge sur son site...