|
« Racine » d’un nombre…
Il ne s’agit pas de la racine carrée, mais du nombre qu’on obtient en additionnant tous les chiffres de l’écriture, et en répétant éventuellement cette opération plusieurs fois jusqu’à obtenir un nombre de 1 à 9. Exemple à partir de 583, on calcule 5+8+3 =16, puis 1+6 = 7, et on dit que 7 est la « racine » du nombre 583.
On constate facilement que les puissances de dix (10, 100, 1000, etc.) ont toutes pour racine le nombre 1.
Quand on divise une puissance de dix par 9, la division entière ne tombe pas juste, le quotient s’écrit uniquement avec des chiffres 1, et on trouve toujours pour reste le nombre 1 : ainsi 10 = 9 x 1 + 1 ; 100 = 9 x 11 +1 ; 1000 = 9 x 111 + 1.
Des nombres comme 40, 300, 8000 ont pour racine 4 ou 3 ou 8 mais les restes dans leur division par 9 sont aussi :
4 (car 40 = 10 x 4 = (9 + 1) x 4 + 4 = (9 x 4) + 4)
ou 3 (car 300 = 3 x (99 + 1) = 3 x 99 + 3 = (3 x 9 x 11) + 3 = (9 x 33) + 3 )
ou 8 (car 8000= 8 x 999 + 8 = 8 x 111x 9 + 8 = (9x 888) + 8).
On peut alors se demander si la racine d’un nombre n’est pas la même chose que le reste de la division de ce nombre par 9. En effet, prenons par exemple le nombre 3486 :
- le reste de la division par 9 de 3486 = 3000 + 400 + 80 + 6 peut s’obtenir à partir des restes des divisions de 3000, de 400, de 80, de 6 soit 3, 4, 8, 6
- on obtient 3+4+8+6 = 21, qu’on remplace par 21 - 2 x 9 = 3, ce qui correspond à chercher la racine de 3486 ou de 21 qui est 3.
On sait qu’un nombre est divisible par 9 si et seulement si la somme de ses chiffres est divisible par 9. Quand le nombre n’est pas nul, cette somme ne peut être zéro. Les multiples (sauf 0) de 9 ont tous pour racine 9 : ainsi 18, 27, 36, 45, 63, 72, 81, 90, 99, 108, 117, etc.
Il y a donc en fait une petite différence entre les deux notions de racine et de reste dans la division par 9 :
- quand le nombre est divisible par 9, le reste est 0 alors que la racine du nombre est 9.
- dans le cas où le nombre n’est pas divisible par 9, la racine d’un nombre est la même chose que le reste de la division de ce nombre par 9.
 Imaginez maintenant une pyramide construite à partir de sa base ainsi : chaque nombre est la somme des deux nombres de la ligne du dessous sur lequel il s’appuie : c = a+b
Un magicien vous propose un jeu :
Exemple : 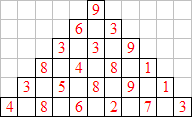 - au lieu d’écrire les sommes d’étage en étage, écrivez plutôt la « racine » entre 1 et 9 de la somme des nombres du dessous ( pour ne pas avoir à écrire de trop grands nombres dans la pyramide).
Ce jeu peut être présenté comme un tour de magie montrant l’habileté et la rapidité en calcul mental du magicien… Le magicien va trouver plus vite que vous le nombre qui sera au sommet ! Il l’écrira même instantanément après que le dernier des 6 nombres que vous aurez choisis sera inscrit à la base de la pyramide ci-dessous…
Comment le magicien fait-il ? Saurez-vous résoudre cette énigme ?
Solution : On appelle a, b, c, d, e, f les six nombres de base, et on construit la pyramide.
Le nombre au sommet se calcule par la formule : a+5b+10c+10d+5e+f . Mais un nombre de forme « a + 5b + 10c + 10d + 5e + f » aura même racine que « a + 5b + c + d + 5e + f ». Le magicien additionne les nombres du bas sauf le 2è et le 5è. Ceux-ci, il les ajoute entre eux, multiplie leur somme par 5, et ajoute ce résultat au total précédent. Dans notre exemple ci-dessus, le magicien ajoute 4 + 6 + 2 + 3 = 15, puis fait 5 (8 + 7) = 75, et obtient : 15 + 75 = 90 soit la racine 9.
Dominique SOUDER
|
