|
Si vous désirez revoir le texte des questions,
c'est ici :
|
|
| E1 |
Les marrons ronds d’Arnaud
Il y a
« équilibre » entre les valeurs des
marrons d’Arnaud et ce que propose Sophie.
Représentons-nous ces deux possibilités sur les deux
plateaux d’une balance qui sera en équilibre.. Enlevons un
cornet de marron rond de chaque plateau. L’équilibre est
maintenu et j’ai maintenant 1,5 cornet qui équilibre 3
euros,… donc un cornet vaut 2 euros.
|
| E2 |
Loups, moutons et serpents.
Ce petit problème
pouvait vous apparaître au premier abord comme ardu. Il
n’en est rien ! La population d’animaux de ce
pré peut être parfaitement décrite par un simple
triplet de nombres, par exemple, d’abord le nombre de moutons,
celui de loups, celui de serpents. Ainsi le soir du dernier jour, la
situation donne le triplet : 1, 0 ,0. La veille au soir elle
était donc de 2, 1, 1, l’avant-veille de 3, 2, 2 Et le
jour précédent ? Et celui qui encore le
précédait ?... Le soir du premier jour la situation
était donc 15, 14, 14, et à l’aube elle était de 16, 15 , 15.
|
|
E3
|
Un grand cœur
Je pense que vous avez trouvé 25 !!
|
| E4 |
Nombre de 2 chiffes.
L’addition de deux
nombres qui sont les images-miroirs l’un de l’autre fournit
nécessairement un nombre (et notre texte exige qu’il ne
possède que deux chiffres) dont les deux chiffres sont
identiques ! Le nombre 11 ne peut être pris en compte
(pourquoi ?) Les seuls nombres que nous pouvons obtenir sont donc
22, 33, 44, 55, 66, 77, 88, et 99 soit 8 nombres.
|
| E5 |
Le vieux coq Luc louche !
Et s’il ne louchait
pas !!! Il verrait donc bien 7 têtes et 20 pattes ce qui
nous donne les situations envisageables que je présente dans un
tableau ; j’envisage toutes les solutions de 7 têtes
avec au moins 1 lapin et 1 poule. Je calcule alors le nombre de pattes
et seule(s) la (ou les) situation(s) avec 20 pattes pourront être
retenue(s).
| Lapins |
1 |
2 |
3 |
4 |
5 |
6 |
| Poules |
6 |
5 |
4 |
3 |
2 |
1 |
| Nb de pattes |
16 |
18 |
20 |
22 |
24 |
26 |
et seule la situation qui
convient est celle avec 3 lapins et 4 poules Mais, Luc louche et la
situation réelle est donc de 3 poules et 4 lapins et Jean Claude compte donc 22 pattes.
|
| PC1 |
LE DODECAGONE DE KEVIN.
Un dodécagone a 12
sommets et 12 côtés. De chacun des 12 sommets
« partent » 11 cordes . Attention, en
écrivant cela, chaque corde est tracée comptée
deux fois : le nombre de cordes est donc de (12 x11) /2 = 66. 12
de ces cordes sont les côtés du dodécagone. Nous avons donc 66 – 12 = 54 diagonales.
|
| PC2 |
AUTRE POLYGONE.
Le plus simple est peut être de compter les diagonales de polygones en nombre croissant de côtés !
Le triangle : 0 diagonale, le quadrilatère : 2, le
pentagone : 5, l’hexagone : 9, l’heptagone :
14, l’octogone : 20.
|
| PC3 |
ISABELLE ET OLIVIER.
Ce texte fait
référence à trois périodes de la vie de ces
enfants. Aujourd’hui, dans 5 ans, il y a 5 ans. Dans 5 ans ils
auront ensemble 35 ans. Aujourd’hui, ils ont donc ensemble 25 ans
et il y a 5 ans, ils avaient donc ensemble 15 ans. . Isabelle avait
donc 10 ans et Olivier 5 ans Aujourd’hui, Isabelle a donc 15 ans et Olivier 10 ans..
|
| PC4 |
PYRAMIDES.
Difficile en apparence. Nous
vous rappelons tout d’abord la signification du signe
« = ». Lorsque vous rencontrez une
égalité numérique, il faut bien comprendre que ce
qui est à gauche du signe « = » et ce qui
est à droite désignent le même nombre, que vous
avez donc deux écritures d’un même nombre, ou si
vous préférez que l’une est une
réécriture de l’autre et dans tout calcul, vous
pourrez utiliser au choix l’une ou l’autre de ces
écritures.
Première
pyramide : ah que ce serait simple si le texte vous avait fourni
ce nombre « a » ;Et bien nous allons le
trouver simplement.
Nous pouvons écrire b
= 12 x a (que nous écrirons plus simplement b = 12a).. De
même c = 6a et comme bc = 16200, nous obtenons 12a x 6a = 72 aa =
16200 Il vient alors aa = :16200 : 72 = 225 et donc a vaut 15.Il est immédiat alors de calculer b et c ; b = 12 x 15 = 180 et c = 6 x 15 = 90.
Voici les petites secrets de
notre première pyramide connus (remarque :
l’écriture axa est souvent noté a2 que l’on lit « a au carré ».
Deuxième pyramide : Nous voyons immédiatement que g = 3 et que d = 90..
6e = 90 donne e = 15.
3h = 15 donne h = 5 et f = 35.
Cette pyramide était peut être plus simple que la précédente.
|
| GC1 |
DECOUPAGE D’UN CARRE.
Le carré ABCD est
composé de 9 polygones dont le carré central. Choisissez
un des trapèzes rectangles et un (parmi les deux) triangle qui
le borde. Sauriez- vous voir qu’en prenant ce trapèze et
ce triangle et en les assemblant autrement, on obtient exactement un
carré, le même que le carré central. Et vous pouvez
répéter cette opération pour chaque
trapèze. Vous venez donc de montrer que le carré ABCD est
composé de 9 pièces qui ont la même aire que cinq
fois celle du carré central.. Le carré ABCD a une aire de 25 cm2. Celle du carré central est donc de 5 cm2
|
| GC2 |
ILS ONT BEL AIR.
Chimène et Ulysse sont
donc deux triangles isocèles. Une des façons les plus
simples de comprendre ce petit texte (sans utiliser de nombres) est
peut être celle-ci.
Vous allez tracer un losange
en commençant par tracer ses deux diagonales de longueur
fortement différentes, puis vous supprimerez un de ces
côtés. Vous avez donc sur votre dessin 3 triangles
rectangles superposables qui réunis par 2 vous donnent bien 2
triangles isocèles. Les voyez-vous ? Ils ont nécessairement même aire puisque formés de deux triangles superposables ! Et pourtant, ils ne se ressemblent pas !!
Il resterait à
légitimer le choix que fit l’auteur des deux triplets de
nombres 41, 41,80 et 41, 41 18. Nous avons tout simplement
recherché les dimensions d’un triangle rectangle,
dimensions en nombres entiers. Et nous avons choisi le triplet 41, 40,
9 qui nous a fourni les dimensions des triangles isocèles. (Si
vous recherchez d’autres triplets « pythagoriques »,
voyez donc dans votre revue « Les héritiers
d’Archimède », sur notre site, le texte T 92).
|
| GC3 |
LES CARRES DE CARO
Le théorème de Pythagore nous garantit l'égalité des aires blanches et rouges.
Nous allons nous
intéresser à l'égalité des aires bleues et
blanches. Il s'agit de trouver cinq nombres entiers positifs
consécutifs. Nommons ces nombres (n-2), (n-1), n, (n+1) et (n+2)
avec n>2 (pour que tous les nombres soient positifs).
La somme des aires des trois
petits carrés doit être égale à celle des
deux plus grands. Cela nous donne l'équation : (n-2)² +
(n-1)² + n² = (n+1)² + (n+2)² Développons :
n² – 4n + 4 + n² – 2n + 1 + n² = n² +
2n + 1 + n² + 4n + 4 (*) soit : - 4n – 2n + n² = 2n +
4n en éliminant les termes identiques dans chaque membre de
l'équation puis - 4n – 2n + n² – 2n – 4n
= 0 en transposant et : n² – 12n = 0 en réduisant
enfin : n (n –12) = 0 en factorisant n Il faut qu'un des deux
facteurs du membre de gauche soit nul c'est-à-dire n = 0 ou n =
12 or n>2 donc la seule possibilité est d'avoir n = 12
Les cinq nombres consécutifs sont alors : 10; 11 ; 12; 13 ; 14
On vérifie aisément que 10² + 11² + 12² =
13² + 14² = 365 où l'on retrouve le nombre de jours de
l'année 2007 qui, est-il besoin de le rappeler, n'est pas
bissextile. Les élèves de 4ème ne connaissent
pas encore les identités remarquables (cela ne saurait tarder,
rassurez-vous).
Pour développer
(n-2)² il suffit de procéder ainsi : (n-2)² = (n-2)
(n-2) = n × n – n × 2 – 2 × n + 2 ×
2 = n² – 4n + 4 De même, (n-1)² = n² –
2n +1 ; (n+1)² = n² + 2n +1 et (n+2)² = n² + 4n + 4
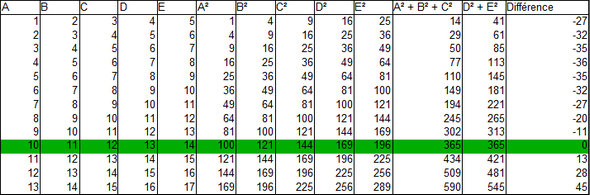
Les petits génies de
l'informatique auront peut-être procédé autrement :
à l'aide d'un tableur on complète la feuille de calcul
ci-dessous en 2 minutes chrono ! L'inconvénient de cette
méthode est qu'elle ne nous garantit pas l'unicité de la
solution.
|
| GC4 |
Il NE FAIT PAS FROID
Une indication nous est
donnée. Bien vraisemblablement, nous aurons des
températures négatives. Pas 1 température, ni 3,
car alors le produit serait impair, mais 2 ou 4 températures.
Par tâtonnements certes, j’ai trouvé ces 5
températures -2, -1, 1, 2, 3.
|
| GC5 |
UN HERITAGE EQUITABLE
Ce problème, le
dernier proposé aux grands élèves de
collèges ne semble pas simple. Mais il est parfaitement
résoluble pourvu qu’on lise bien
l’énoncé, qu’on le traduise en
égalités, que l’on sache faire quelques
opérations de soustraction et de division par 10 et aussi et
surtout que l’on se donne une méthode de recherche. Nous
allons bien développer un corrigé de cet exercice,
corrigé qui est parmi les plus simples. Nous vous demandons la
valeur de l’héritage (que j’appellerai h) et le
nombre de partages (que j’appellerai n). Il existe une relation
assez simple entre ces valeurs. Le quotient de h par n nous donne la
valeur unique de chaque part (que j’appelle p).
L’égalité h = p x n nous permet dès que deux
des nombres h, p et v sont connus de calculer le troisième !
Lisez bien ce qui suit sans vous occuper des calculs que vous reprendrez après.
L’énoncé
nous permet de calculer, en fonction de h, la première part et
nous précise aussi que toutes ces parts sont égales. Nous
allons calculer quelle est la part P1 qui revient au premier, puis en
fonction du reste que nous calculerons facilement, quelle est la part
P2 du second,… et nous dirons que ces parts sont égales !
Le premier enfant prend 100 euros et le 1/10 du reste. La part P1 du
premier est 100 + (h – 100) / 10 = 90 + h / 10 Le Reste R1
après cette prise est alors de h – (90 + h / 10) = h
– 90 – h / 10 = 9 h / 10 - 90 Calcul identique pour le
second ; déduisons d’abord les 200 euros puis calculons le
1 /10 de ce qui reste. P2 = 200 + (R1 – 200) / 10 = 200 + (9h /
10 – 90 – 200) / 10 = 200 + 9h / 100 – 29 = 9h / 100
+ 171 Ecrivons que ces parts sont égales : 90 + h / 10 = 9h /
100 + 171, h/10 – 9h/100 = 171 -90 h/100 = 81 h = 8 100
Et le tour est joué !
Le premier prend 100 euros + le 1/ 10 de ce qui reste, reste qui vaut
(8 100 – 100) / 10 = 800. et P1 =.100 + 800 = 900 Chaque part
étant égale, nous avons donc 8 100 / 900 = 9 parts Valeur de l’héritage : 8 100 Nombre d’héritiers :9
et je vous propose maintenant , dans un tableau de contrôler tout ceci :
| Part n° |
Calcul |
Reste |
| 1 |
100 + (8100 – 100) / 10 = 900 |
7200 |
| 2 |
200 + (7 200 – 200) / 10 = 900 |
6300 |
| 3 |
300 + (6 300 – 300) / 10 = 900 |
5400 |
| 4 |
400 + (5 400 – 400) / 10 = 900 |
4500 |
| 5 |
500 + (4 500 – 500) / 10 = 900 |
3600 |
| 6 |
600 + (3 600 – 600) / 10 = 900 |
2700 |
| 7 |
700 + (2 700 – 700) / 10 = 900 |
1800 |
| 8 |
800 + (1 800 – 800) / 10 = 900 |
900 |
| 9 |
900 + (900 – 900) / 10 = 900 |
0 |
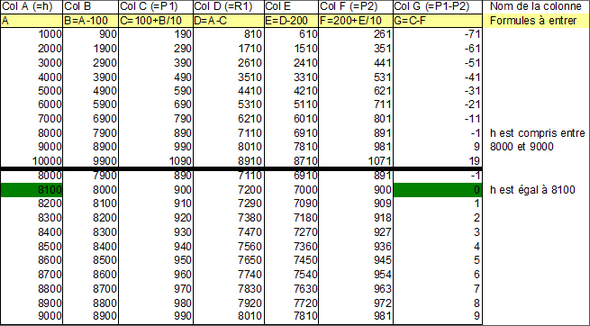
Comme pour GC3, on peut également
résoudre l'énigme à l'aide d'un tableur (sans
garantie d'unicité):
|
|
|



