Dans un triangle rectangle, le carré de l’hypoténuse égale la somme des carrés des côtés de l’angle droit.

Ce théorème simple de compréhension est attribué à Pythagore quoiqu’il fut probablement connu avant lui. (voir le chapitre 14 du livre « Jeux mathématiques du Scientific American » édité par l’ADCS. ce chapitre est intitulé « Le pont aux ânes » nom que l’on donnait jadis, au lycée, à ce théorème. Qui ne le comprenait pas, était un âne)

Une des démonstrations particulièrement éloquentes se compose de deux dessins que nous vous fournissons.

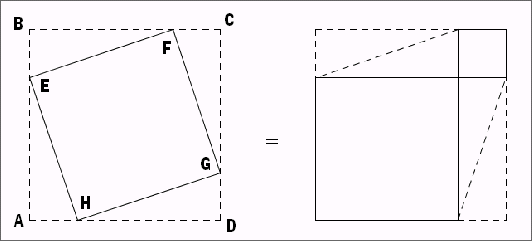
Figure 1 : On dessine un carré ABCD. On choisit un point E sur le côté AB et les points F de BC, G de CD, H de DA tels que les segments AE,BF, CG, DH aient même longueur. Nous obtenons un carré EFGH (démontrez que nous avons bien un carré) bordé de 4 triangles rectangles égaux.

Figure 2 : Comme dans un puzzle, nous allons assembler les 5 morceaux du grand carré en regroupant par deux les triangles rectangles, donc pour obtenir deux rectangles. Otons de ces deux grands carrés les 4 triangles rectangles. Il vous reste d’une part, le carré construit sur l’hypoténuse (figure 1), d’autre part les deux carrés construits sur les côtés de l’angle droit du triangle (figure 2)..

Parmi les triangles rectangles dont les côtés sont des nombres entiers, vous connaissez tous le triangle rectangle de côtés 3, 4, 5. , qui est d’une part le plus petit (de plus petite hypoténuse si vous préférez) triangle rectangle « en nombres entiers », mais aussi le seul dont les côtés sont des nombres consécutifs.

Il existe une infinité de triangles rectangles en nombres entiers. Et lorsque vous connaissez les dimensions de l’un d’entre eux, il vous est immédiatement possible d’en avoir une infinité (comme dit mon ami photographe, chacun est un agrandissement de l’autre).. Multipliez chacun des côtés par un même nombre.

Nous vous proposons ce jour la liste de tous les triplets de « nombres pythagoriciens » (triplets de nombres entiers qui sont les côtés d’un triangle rectangle) dont le plus grand est inférieur à 1 000, triplets que nous appellerons primitifs parce que ses trois nombres ne sont pas divisibles par un même nombre ils sont premiers entre eux)..