|
Vous avez déjà
vu ces belles constructions en tiges légères , avec
des fils très fins auxquels sont accrochées des masses.
L'ensemble paraît si fragile et pourtant l'équilibre
est bien là !
Ces mobiles doivent
avoir leurs tiges horizontales et, bien entendu, leurs fils verticaux.
De plus les masses des tiges et des fils sont considérées
comme négligeables.
 |
Ce
premier mobile vous est entièrement décrit par
la connaissance des masses accrochées et par les proportions
des longueurs des bras de levier . |
Sur les schémas
suivants, les masses (toutes avec la même unité) sont
notées par des majuscules A, B, C, … ; les longueurs
(toutes avec la même unité) sont notées par
des minuscules a, b, c,…. Pour des raisons de place les segments
horizontaux ,qui ne sont pas représentés à
l'échelle, sont indiqués en pointillés.
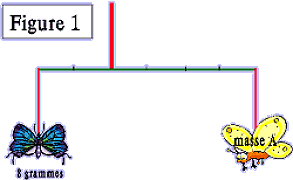
Calculer la masse A |
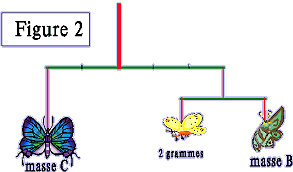
Calculer les masses
B et C.
|
|
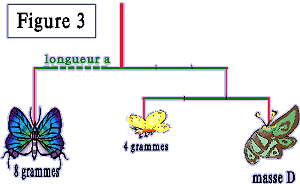
Calculer la masse
D et la longueur a.
|
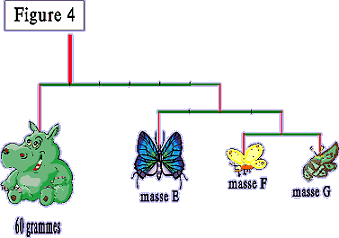
Calculer les masses
E,F et G.
|
Vous noterez que
ces équilibres font intervenir à la fois masse et
distance au centre de sustentation .
C'est au grand savant
Archimède, auteur en particulier d'un long texte sur
l'équilibre des figures planes, que l'on prête
la célèbre formule " Donnez-moi un point
d'appui et je soulèverai le globe "
|
 |
Archimède est actuellement bien connu
puisque ses oeuvres complètes sont publiées en édition
bilingue (français-grec) à la société
d'édition " Les belles lettres " à Paris
(voyez votre CDI !)
Archimède est considéré
comme l'un des plus grands scientifiques de tous les temps. "
Si les mathématiques de la Grèce avaient suivi Archimède
plutôt qu'Euclide, Platon et Aristote, ils auraient devancé
de deux mille ans l'ère des mathématiques modernes
". (Cité par Audirac aux éditions Magnard).
Aujourd'hui, nous nous bornerons à
ne citer qu'un seul de ses travaux. Le nombre appelé aujourd'hui
PI qui est le rapport entre la longueur d'un cercle et celle de
son diamètre :
3+1/7 > PI > 3+1/(7+1/10).
Un élève de classe de 3ème
pourvu qu'il ait une calculatrice dotée des fonctions sinus
et cosinus n'aura aucune difficulté à approcher par
calcul, avec la précision qu'il souhaite ce nombre.
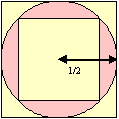 |
Inscrivez dans un cercle de rayon 1/2
un carré puis construisez un nouveau carré qui
circonscrit ce cercle (le périmètre du cercle,
qui vaut exactement PI, est compris entre les périmètres
de ces carrés).
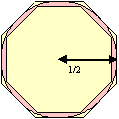
Doublez le nombre de côtés
de ces deux polygones réguliers. Vous obtiendrez deux
octogones et une meilleure approximation de PI ; doublez encore,
...
|
 |
Prépare une belle frise : En cadeau,
nous vous offrons avec cette première épreuve 2001-2002
du Grand Prix Edouard Lucas, les 50 premières décimales
du grand nombre PI ; 25 autres suivront avec chaque épreuve
:
14159 26535 89793 23846 26433 83279 50288
41971 69399 37510
| Voici les réponses à
cette gentille rubrique des mobiles : A = 4 ; B = 2 ; C = 6
; D = 8 ; a = 4,5 ; E = 6 ; F = G = 3 |
|



