Archimède, géomètre syracusain -Musée de Picardie Statue de bronze de 1,15m de T. Caudron (1805-1848). Actuellement, cette statue est visible à l'Institut Universitaire de Formation des Maîtres d'Amiens. Il reste d'un homme ce que donnent à songer son nom, et les oeuvres qui font de ce nom un signe d'admiration, de haine ou d'indifférence. Paul Valéry (1871-1945)

Archimède comme de nombreux savants de l'antiquité pratiquait plusieurs sciences ; il était à la fois géomètre, arithméticien, physicien et philosophe. C'est l'un des plus grands génies scientifiques de tous les temps et pour citer l'Américain E.T. Bell, " Son génie lui aurait permis, si il était né plus tard, de mieux comprendre Einstein que les grands scientifique du 20ème siècle le comprenaient eux-mêmes ".

Nous ne connaissons pratiquement rien de sa vie, et nous ne savons pas, par exemple, s'il a été marié, s'il a eu des enfants ! Nous savons par contre qu'il vécut à Syracuse, colonie grecque en Sicile. Son décès est connu ; il fut en effet tué par un soldat romain de Marcellus pendant la deuxième guerre punique, en 212 avant J.C. Son année de naissance est estimée à - 287 avant J.C.

 

On ne trouve aucune trace chez les contemporains d'Archimède de ses exploits qui lui furent souvent attribués quelques siècles plus tard. Le patriote qui défend sa cité attaquée par des légions romaines a-t-il bien inventé les balistes ou catapultes permettant aux Syracusains de " bombarder " la flotte ennemie depuis le haut des murailles ? Le mécanicien spécialiste des leviers (voir texte T6) a-t-il créé ces mains de fer attachées à une chaîne et qui étaient jetées sur les navires ennemis, les saisissant par la proue, les élevant à la verticale en utilisant un levier et un énorme contrepoids, pour les laisser brutalement tomber ? ... On lui attribue également la création d'énormes miroirs ardents qui en concentrant les rayons du soleil sur leur surface concave lui permettait d'incendier la flotte ennemie. Bien des écrits ont été faits à ce sujet et Buffon, en 1747, a construit un miroir composé de 138 petites glaces lui permettant d'enflammer des pièces de bois situées à bonne distance. Archimède a-t-il aussi réussi à faire tirer par un seul homme une galère chargée ?

Fort heureusement pour nous, il laisse de très nombreux documents sur ses travaux. Ces écrits attestent donc du génie de cet " immense" mathématicien et ingénieur et nous allons vous présenter les résultats connus et simples, après avoir dit quelques mots de " La légende d'Archimède ".

La légende nous dit que Hiéron, tyran de Syracuse voulait offrir une couronne d'or à Jupiter. Mais il soupçonna très vite son orfèvre d'avoir réalisé ce joyau en alliant de l'argent à de l'or. Il était hors de question de détruire cette couronne, et pour en avoir le cœur net, Hiéron posa ce problème à Archimède.

C'est en prenant un bain qu'Archimède fut amené à réfléchir sur le fait que ses pieds flottaient et comprit d'un fait bien banal ! ... que le bain pouvait être une " balance à évaluer les volumes ". Tout entier aux joies de sa découverte, il courut nu, dit-on, jusque sa table de travail en criant " EUREKA, EUREKA " (c'est à dire j'ai trouvé, j'ai trouvé), dans les rues de la ville. Les élèves de nos collèges ont aussi pu mettre en évidence ce qui est pertinent dans cette poussée, à savoir qu'elle dépend exclusivement de la densité du fluide dans lequel on immerge le corps et du volume de sa partie immergée

Voici quelques données et séries d'expériences :

Le matériel nécessaire est peu coûteux.

Le principe en 3 expériences.

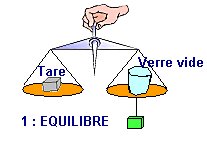
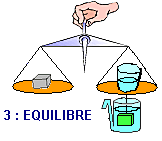
On équilibre par une tare sur un plateau de balance, un verre vide et une masse suspendue à l'autre plateau. On dispose aussi d'un vase à trop plein rempli d'eau.	On ôte le verre afin qu'il puisse récupérer l'eau du vase. On immerge le corps. L'équilibre est détruit dès l'immersion et reste détruit après l'écoulement d'eau.	On réinstalle le verre sur le plateau. on obtient de nouveau l'équilibre, et par comparaison avec ce qui précède, il apparaît bien que la masse immergée a bien reçu une force qui s'oppose exactement au poids du volume d'eau du corps immergé.

Nos jeunes lecteurs peuvent facilement calculer le volume de la couronne, sa masse si elle était tout en or ou tout en argent, et en conclure ... que le bijoutier était un gredin.

Les élèves des grandes classes de collège sauront calculer les masses d'or et d'argent de cette couronne (3505,71 g d'or et 674,31 g d'argent). A ce propos, une remarque très importante : on peut dire que cette couronne de 4180 g dont 3505 g sont en or titre 0,83 ou 830 millièmes. Les bijoutiers utilisent couramment le carat qui a deux significations très précises (voir le dictionnaire Robert. Dictionnaire d'orthographe et d'expression écrite de André Jouette). " Le carat métrique (ou carat poids) vaut 0,20 g et sert pour peser diamants, pierres précieuses et perles fines. Le carat (ou carat titre) indique une proportion. Il vaut 1/24 de la masse totale d'un alliage d'or. Une bague de 18 carats n'a donc en or que les ¾ de son poids en or fin ".

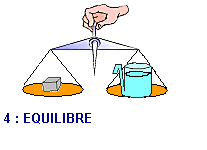
La réciproque en 2 expériences:

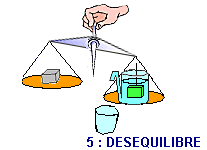
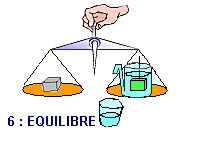
On équilibre un vase à trop plein rempli d'eau par une tare.	On immerge alors un corps suspendu par un fil. On observe un déséquilibre immédiat...	...qui diminue au fur et à mesure que l'eau s'écoule et qui cesse (fig 6) en même temps que cet écoulement.

Le poids de l'eau écoulée est exactement compensé par une action (une réaction) de l'eau du vase.

Commentaires:

La conclusion de l'expérience 3 constitue le célèbre "Principe d'Archimède" que nous pouvons énoncer ainsi: Tout corps plongé dans un fluide reçoit de la part de celui-ci une poussée verticale, dirigée de bas en haut, appliquée au centre de gravité du corps, et qui est égale au poids du fluide déplacé.

Vous connaissez toutes et tous de multiples applications de ce principe telles le sous-marin, l'aérostat,...

La conclusion des expériences 4 à 6 constitue bien la réciproque qui peut s'énoncer ainsi : Tout corps immergé dans un fluide exerce sur celui une poussée opposée à la poussée d'Archimède reçue.

Mais outre le petit problème posé quant à la teneur de cette couronne de Hiéron en or et en argent, nous pouvons aussi vous poser le problème de la recherche d'applications pratiques de cette réciproque.