|
Si vous désirez revoir le texte des questions,
c'est ici :
|
|
| E7 |
Le plus simple est de faire 50 déplacements. Appelons
1 le plus petit disque, 2 celui immédiatement plus
grand, 3 ... Voici dans l'ordre les disques transportés
jusqu'au 50ème :
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1
2 1 6
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2
Donc le 50ème disque transporté est le numéro
2.
|
| E8 |
Les chiffres inconnus marqués par de " . "
ne sont pas tous indispensables.
- Le " c " est immédiatement connu. C'est
" 4 " (parce que 9 x 6 = ?).
- Puis essayons la première division en ligne :
646 : . 9 = . .
Le chiffre des dizaines du diviseur peut-il être 1
?
646 : 19 = 34 ! OUI
Peut-il être 2 ou 3 ou ... 5 ? NON
De proche en proche, vous découvrez les chiffres inconnus.
- Sur le schéma suivant, en petits caractères
nous vous indiquons l'ordre de découverte de chiffres.
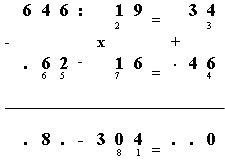
Et après la découverte notée 7, on effectue
enfin la multiplication de 19 par 16 et on obtient la réponse
demandée : 304
a b c ... c'est 304
|
| E9 |
Reprenons les affirmations dans le même ordre :
1 boîte de macarons coûte 1,5 gâteau,
1 pâté de canard coûte 1 gâteau et
2 euros,
1 boîte de macarons coûte 1 pâté et
2 euros,
donc 1 boîte de macarons coûte 1 gâteau et
4 euros,
donc la moitié d'un gâteau coûte 4 euros,
le gâteau vaut 8 euros.
A partir de là, le pâté vaut 10 euros et
la boîte de macarons vaut 12 euros ?
Réponse :
1 macaron vaut 12 euros
1 pâté vaut 10
euros
1 gâteau vaut 8 euros
|
| C7 |
Difficile d'aspect, mais simple à réaliser.
Pour h, essayons consécutivement les chiffres 1, 2,
3, ...7 (grosse surprise, mais impossibilité), 8, et
enfin 9 pour h,
La multiplication complète est donc :
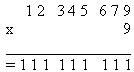
a vaut donc 1.
|
| C8 |
Louise a donc un chien, un chat, un poisson, un hamster,
c'est à dire 4 amis.
Et vous ? |
| C9 |
Vous savez calculer l'aire d'un carré ; si l'on vous
donne la mesure a de son côté.
Et si l'on vous donne la mesure de sa diagonale ! Alors, un
simple petit dessin suffit !
20022 = 4 008 004
La moitié du carré de 2004 de diagonale est
2 008 008.
La somme des aires des 4 triangles est 1 999 996,
dont le quart demandé est (en cm2) de 499
999.
|
|



