|
Horizontalement
1 CLAIE - MATIN ; 2 RAS - ALE ; 3 OS
- MA - EN - ER ;
4 CATALAN ; 5 PAIN - VAIN ; 6 GNOME ; 7
LIEE - TROC ;
8 HUMECTE ; 9 TA - RU - RE - SA ; 10 RIT
- MAL ;
11 ELEVE - EPICE.
|
Verticalement
1 CROUP - LITRE ; 2 LAS - AIL - ; 3
AS - CI - EH - TE ;
4 MANGEUR ; 5 EBAT - MUSE ; 6 ATOME ;
7 MIEL - CRIE ; 8 NAVETE ; 9 TA - NA - RE
- MI ;
10 ILE - SAC ; 11 NERON - CHALE.
|
Problème 1 : Le loup, la chèvre
et les choux.
L'homme a pu reprendre sa route avec sa suite au complet après
7 traversées de la rivière. En veillant bien à
ce que le loup ne reste pas sans surveillance avec la chèvre
et que la chèvre ne reste pas seule avec les choux, voilà
une solution :
|
N°
|
Action |
Résultat
L : Loup.
X : Choux.
V : Chèvre.
H : Homme
|
|
1
|
L'homme emmène la chèvre |
LX > VH |
|
2
|
L'homme revient seul |
LXH < V |
|
3
|
L'homme emmène le loup |
X > LVH |
|
4
|
L'homme revient avec la chèvre |
XVH < L |
|
5
|
L'homme laisse la chèvre et emmène
les choux. |
V > LXH |
|
6
|
L'homme revient seul |
VH < LX |
|
7
|
L'homme emmène la chèvre |
> LXVH |
|
Problème 2 : Quelle femme fantastique ! Connaissez-vous
Marie Curie ?
|
|
|
M
|
A
|
R
|
I
|
E
|
|
+
|
|
C
|
U
|
R
|
I
|
E
|
|
|
|
|
|
|
|
|
|
|
R
|
A
|
D
|
I
|
U
|
M
|
|
|
|
|
4
|
3
|
1
|
2
|
7
|
|
+
|
|
9
|
5
|
1
|
2
|
7
|
|
|
|
|
|
|
|
|
|
|
1
|
3
|
8
|
2
|
5
|
4
|
|
|
Problème 3 : Je vous reçois 5 sur 5.
Voici une solution avec 11 " 5 " :
(5x5x5) x (5+5+5+(5 :5)) + (5+5) :5 = 625x16 + 10 :5 = 2000
+ 2 = 2002
Qui peut faire mieux ?
|
Problème 4 : Nombres croisés.
|
Problème 1 : L'étoile magique
.
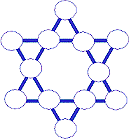 Aux
12 sommets de cette étoile, écrire un nombre compris
entre 1 et 12 (chacun de ces 12 nombres est utilisé une
seule fois), de sorte que la somme de 4 nombres alignés
soit la même sur chacune des 6 branches de cette étoile.
|
Problème 2: La piscine.
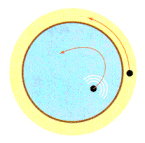 Un
nageur se trouve dans un bassin circulaire.
Sur le bord de ce bassin, un coureur veut l'empêcher de
sortir de l'eau. La vitesse du coureur est triple de celle du
nageur.
Le nageur peut-il trouver une stratégie qui lui permette
d'atteindre un point du bord du bassin avant l'arrivée
du coureur et ceci quelles que soient les positions initiales
des deux sportifs ?
Défendez votre point de vue. (les deux sportifs sont
assimilés à des points)
|
|
Problème 3 : Télépathie ?
 Lors
d'un numéro de music hall, un illusionniste prend à
partie un spectateur dans la salle :
- " Bonjour ! monsieur, voulez-vous, dans le plus grand
silence, effectuer les opérations que je vais vous
demander puis annoncer au public et à moi-même
votre résultat ?
- " Le spectateur : Tout à fait d'accord !
- " L'illusionniste : Multipliez votre âge par
2, ajoutez 6, multipliez le résultat par 50, ajoutez-y
le numéro du département où vous êtes
né, soustrayez le nombre de jours que contient cette
année et annoncez le résultat.
- " Le spectateur : 1248
- " L'illusionniste : Vous avez 13 ans et vous êtes
né dans lles Bouches du Rhône
- " Le spectateur : C'est exact !
Comment fonctionne ce tour ?
|
Problème 4 : The frog and the snake
 One
morning at sunrise, I found a frog and a snake in my garden,
18 m apart and heading for one another. Watching them over
the next few days, I noticed that the frog moved ahead 3.5 m
each daytime and moved back 1 m at night. The snake, being
a more nocturnal creature, moved forward 2.5 m each night-time
and moved back 2 m each daytime.
When and where does the snake catch the frog ?
|
