T 38 - Corrigés de l'étape 1 (2002/2003).
Si vous désirez revoir le texte des questions, c'est ici :
E25

QUI ?
 La réponse est LUCAS. Edouard Lucas est né à Amiens en 1842 et est mort à Paris en 1891. Il vous a été présenté dans votre revue « LES HERITIERS D’ARCHIMEDE » (Texte T 8).
E26

CENT QUATRE

Numéro des dossards
de 1 à 9
de 10 à 19
de 20 à 29
...
de 90 à 99
de 100 à 104
Nombre de 1
1
11
1
...
1
6

Au total, le chiffre 1 a été écrit 26 fois.

E27

&

E28

L'octogone
Les neuf nombres ont pour somme 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. Pour simplifier ce corrigé, nous supposons cet octogone régulier.
Un nombre est écrit au centre du cercle, et pour chacun des huit autres, lui correspond un nombre diagonalement opposé ce qui nous donne quatre alignements de trois nombres (en utilisant celui du centre) de même somme ; les nombres sur le cercle forment donc quatre paires de nombres de même somme.
Ces huit nombres aux sommets de l’hexagone ont pour somme un multiple de 4.
Quel pourrait-être le neuvième nombre « au centre » ?

Nous avons a priori 9 choix 1, 2, 3, 4, 5, 6, 7, 8, 9.

La somme des huit autres nombres est ainsi comprise entre 44 (si le « 1 » est au centre) et 36 (si le « 9 » est au centre) et nous avons donc trois possibilités pour la somme des huit nombres écrits au sommet de l’octogone : 36 ,40 et 44 c’est à dire avec, au centre, les nombres 1,5 ou 9.
D’où ce tableau :

Centre
Somme des deux nombres alignés avec le centre
Paire de nombres alignés avec le centre
Produit de trois nombres alignés
1
11
9 et 2
8 et 3
7 et 4
6 et 5
18
24
28
30
5
10
9 et 1
8 et 2
7 et 3
6 et 4
45
80
105
120
9
9
8 et 1
7 et 2
6 et 3
5 et 4
72
126
162
180

Les produits maximum et minimum sont soulignés.
E29

QUE DE MIROIRS
Un rectangle peut être constitué de 1 miroir au minimum, jusqu'à 7 miroirs au maximum.
Présentons les résultats sous forme de tableau que vous pourrez très facilement vérifier.

Rectangle formé de 1 miroir 2 miroirs 3 miroirs 4 miroirs 5 miroirs 6 miroirs 7 miroirs
Nombre de solutions 7 rectangles 4 rectangles 4 rectangles 1 rectangle 0 rectangle 1 rectangle 1 rectangle

Au total, cela fait bien 18 rectangles.
E30

QUATRE ! NON !
Nous avons bien dit 1 coin, pas 2 !
Cette carte a bien sûr 5 coins !

E31

CRYPTAGE (1)
La réponse est FAITES DES SCIENCES.
E32

ROMAIN ?
Vous avez trouvé ? La réponse était MLXXX.
Multiplions les nombres romains XLV et XXIV. Ce n’est guère facile, n’est-ce pas ?
A moins qu’on écrive ces nombres dans notre bon « jeune » système de numération.


XLV, c’est le nombre 45. Et XXIV, c’est le nombre 24.
45 x 24 = 1080 et 1080 s’écrit, en numération romaine, MLXXX.
C25

104 ... ENCORE !
1, 2, 3 ....... On arrête quand on a écrit le 104ème chiffre 1.

                      TOTAL
Nombres écrits de 1 à 9 de 10 à 19 de 20 à 29 ... de 90 à 99 de 100 à 109 de 110 à 119 de 120 à 129 ... de 150 à 159 de 1 à 159
nombre de 1 1 11 1 ... 1 11 21 11 ... 11 96

Nous approchons de 104, écrivons les nombres suivants : 160, 161, 162, 163, 164, 165, 166.
Ce qui fait encore 8 chiffres 1.
96 + 8 = 104. Nous y voilà ! La réponse est donc 166.
C26

PALINDROMES

Répétition d’un chiffre interdite et nombre à 4 chiffres maximum.
Exemples :

  • 1331 : il y a répétition.
  • 242 : il y a répétition.
  • 55 : il y a répétition.
Il n’y a aucune réponse pour les nombres qui s’écrivent avec 2, 3 ou 4 chiffres. Les solutions sont donc : 0, 1, 2, 3, .... 9. Il n’y a donc que 10 possibilités.
C27 PALINDROMES (ENCORE)
Tous les nombres à un chiffre sont des palindromes, donc 10 possibilités.
Les nombres à deux chiffres identiques, ne se terminant pas par 0, sont des palindromes.
11, 22, 33, ...99. Donc encore 9 possibilités.
Pour les nombres à 3 chiffres, il suffit d’intercaler n’importe quel chiffre dans la liste des palindromes à deux chiffres : 10 x 9 = 90, et voilà 90 possibilités supplémentaires.
Pour les nombres à 4 chiffres, il suffit de compter les nombres à 2 chiffres ne commençant pas par 0 : 10, 11, ...99, il y en a 90.
Et encore 90 possibilités supplémentaires.
Soit au total : 10 + 9 + 90 + 90 = 199. On trouve 199 palindromes.
C28 CRYPTAGES (2)
La réponse est FETE DES SCIENCES.
C29 ANNIVERSAIRE DE L’ADCS
Aucun problème pour les 104 élèves présents au CNAM le samedi 19 octobre, puisqu’ils ont soufflé les 30 bougies du gâteau.
La réponse est 30.
C30 LA RECETTE DES TUILES CHOCOLATEES DE SAINT-LEU
Ecrivons simplement la liste des nombres solutions de chaque comptage.

1) On compte de 2 en 2 en partant de 1 :
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51 ...

2) On compte de 3 en 3 en partant de 2 :
2, 5, 8, 11, 14, 17, 20, 23, 26,29, 32, 35, 38, 41, 44, 47, 50, 53, ...
3) On compte de 4 en quatre en partant de 3 :
3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, ...
N’oublions pas que Léo veut fabriquer le plus de tuiles possibles, mais il n’a pas suffisamment d’ingrédients pour en fabriquer plus d’une cinquantaine. La réponse est donc 47.
C31

CARRES MAGIQUES ET MARCHE DU CAVALIER

La somme magique nous est donnée par celle des nombres d’une colonne, soit : 260

Par simple soustraction, on trouve alors :
A = 63 ; B = 14 ; C = 17 ; D = 36 ; E = 21 ; F = 12 ; G = 59 ; H = 38.

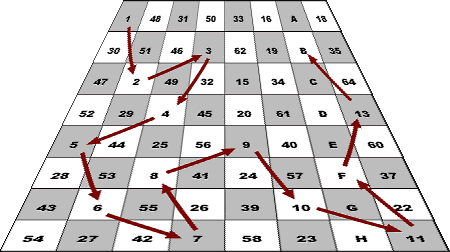Plus astucieux, en utilisant le texte T13 de votre revue « LES HERITIERS D’ARCHIMEDE », on peut contrôler que la suite des 64 nombres correspond à la marche du cavalier. On retrouve alors les nombres A, B, C ...
C32 TALMAS HANOÏ SELECTION
Ce texte très simple a soulevé deux types de questions :
  • Tout d’abord, le texte précise que chaque joueur « pèse » le poids affiché sur son maillot. Et ceci en «unités» non précisées ; Il ne s’agissait pas de kilogrammes ! Il est courant de dire qu’au point de vue fiscal, Monsieur Dupont «pèse» trois fois plus que Monsieur Durand (il paie trois fois plus d’impôts) ou que , pour le conseil d’administration de telle société, Monsieur Arthur qui a quatre fois plus de parts sociales que Monsieur Bernard «pèse » quatre fois plus !
  • Ensuite rien n’indique dans le texte que les équipes d’une sélection sont composées d’un nombre égal de joueurs : Non, ces équipes ont simplement le même «poids» qui est, comme indiqué, la somme des poids de chaque maillot.

La somme des poids des joueurs est 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36 ; chaque équipe pèse donc 18 unités.

Voici donc les sept réponses qui nous donnent les répartitions de nos « Talmasiens »

8 , 7 , 3 et 1 , 2 , 4 , 5 , 6
8 , 7 , 1 , 2 et 3 , 4 , 5 , 6
8 , 6 , 4 et 1 , 2 , 3 , 5 , 7
8 , 6 , 3 , 1 et 2 , 4 , 5 , 7
8 , 5 , 4 , 1 et 7 , 6 , 3 , 2
8 , 5 , 3 , 2 et 7 , 6 , 4 , 1
7 , 6 , 5 et 1 , 2 , 3 , 4 , 8